The assembly-line balancing problem (today SALBP) is a bin-packing problem with precedence constraints, that was invented in the 50s to model and optimize the design of assembly lines.
Because early researchers favored mixed-integer linear programming techniques to solve them, and because MIPs are notoriously bad at managing problems with a time dimension, the assembly line design was mapped into a bin-packing problem that hides the temporal dimension of the problem.
However, modern practitioners have noticed that assembly line problems are complex and often need the time dimension to be explicitly considered.
This has lead to a regain of interest in constraint programming methods for the assembly line problem as they are able to handle complex time-related constraints.
Early papers on assembly line balancing
Early papers like Assembly-Line Balancing by Linear Programming (E. H. Bowman 1960) show that practitioners of that time were trying to solve scheduling and sequencing problems with linear programming.

Similar scheduling problems tackled with linear programming include
- Bowman, Edward H. 1956. “Production Scheduling by the Transportation Method of Linear Programming.” Operations Research 4 (1): 100–103.
- Bowman, Edward H. 1959. “The Schedule-Sequencing problem*.” Operations Research 7 (5): 621–24.

However solving problems with an explicit temporal dimension is difficult with MIP engines as the models tend to have a large number of binary variables and relaxations tend to be very weak.

The assembly line balancing problem avoids the time dimension by eliminating the start times of each task and instead transforming stations into "bins" inside of which the order doesn’t matter.
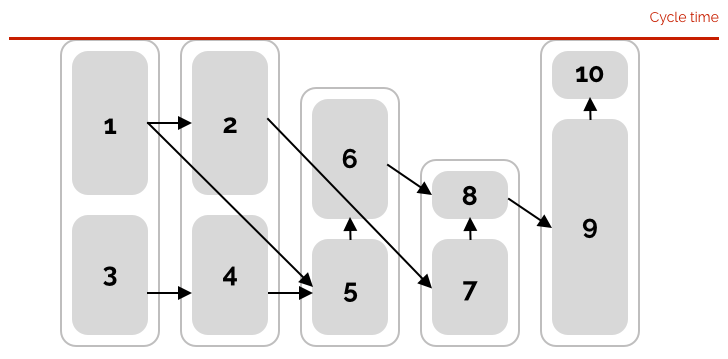
Real world balancing problems
Falkenauer (2005) explains how real-life assembly line problems differ from their mathematical simplifications [2]
- The majority of real life line balancing takes place at an already built assembly plants so the number of stations is fixed and re-balancing is what is needed
- Each station is unique in the tooling and restrictions on the tasks that can be done on it
- There are zoning constraints that should be considered in line balancing
- Since the assembly plants are already built, elimination of stations is not feasible
- Smoothing the workload across stations should be an important objective of the line balance
- Multiple operators usually work in a station, which makes packing approximation within a station very imprecise
- Multiple operators can collaborate on a given task, which means stations themselves need to be scheduled with resource constraints
- Station level ergonomic should be considered which might lead to assignment restrictions and work area interference between workers should be incorporated
- Assembly lines create multiple products, and the balancing needs to be done in average with consideration for peak times
- Some exceptional products are so rare it makes sense to temporarily retarget the stations for this product
Modern approaches to line-balancing problems
Authors like Scholl, Becker and Boysen have worked on solving more realistic assembly line problems (Scholl 1999, Becker and Scholl 2006, Boysen 2007, etc)
They have created a data format to cover all the features they believe are important. This includes among other things
- precedences
- sequence-dependent task lengths
- parallel stations
- specific resources in stations
- task pairs assignment restrictions (same station, different station)
- task-station assignment restrictions
- station load restrictions
- alternative tasks
- mounting positions
- assignment incompatibilities due to mounting positions
Authors like Alghazi and Kurz [3][4] have considered
Zoning constraints
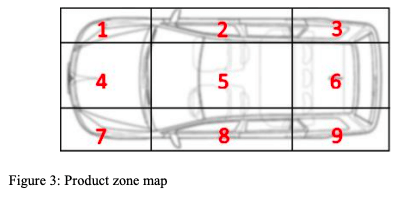
Parallel workers
There are more than one worker per station
Assignment restrictions
Pairs of tasks can be assigned to
- the same station
- different stations
- the same worker * station
- different worker * station
Many constraints like the usage of a heavy equipment, or interference between zones are modeled indirectly via assignment constraints
Ergonomy
Each task has an ergonomy score and each worker * station has a maximum ergonomy score.
The ergonomy score is also used to model complex interactions between tasks within a station * worker
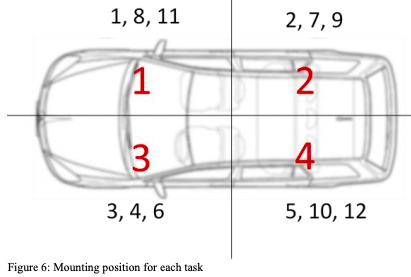
Mounting positions
Models for line balancing
Alghazi compared a MIP model based on the formulation by Becker and Scholl (2009) with a CPO model.
Alghazi comments (page 59 in [3])
Table 7 summarizes the results of both the IP and CP subject to a one hour time limit. Since 10 runs were executed for each instance in CP, the number of runs the given solution (number of workers) was found is also shown. As expected the IP faced difficulties as the size of the instance increases. The optimal solution is found only in 3 small sized instances while no feasible solutions were found on the largest instance of each band within the one hour time limit. On the other hand, the CP managed to find optimal solutions in 10 out of the 12 instances with only a small gap in the solution of the other two instances. In CP instance B1.3 two different solutions were found for different seed runs, of which one is optimal. It is clear that Band 1 instances were difficult for both the CP and IP solvers
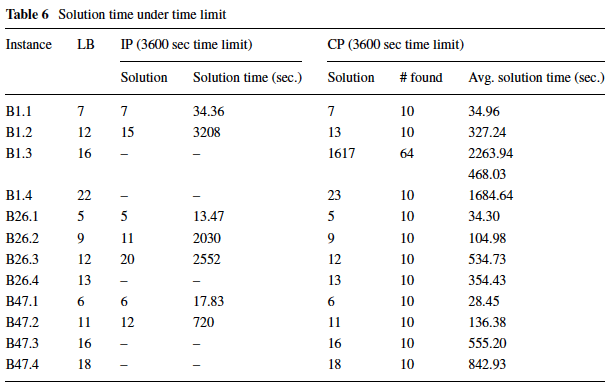
Table 6 from [4], easier to understand than table 7 from [3], globally same content
The full CPO model is provided by Alghazi with the instance B1.1. We were able to make small improvements to the model bringing the time to find the optimal solution of the small instance from 2 seconds to 1 seconds (on our machine) and proving optimality.
Because we only have this small instance, it is impossible to know what would be the impact of our improvements on the rest of the benchmark.
Quick overview of the CPO model
CPO provides interval variables to model any task, activity or element that needs to be scheduled on the time horizon. In this case we want to schedule tasks
dvar interval task [t in tasks] in t.start .. t.end size t.duration;Each task may be done by a combination of a station and a worker. To capture this assignment CPO provides the concepts of optional tasks and alternatives
dvar interval aTask [t in tasks][s in stations][w in workers] optional;
forall (t in tasks) alternative(
task[t],
all (s in stations, w in workers) aTask[t][s][w]
);This means only one aTask can be present and it needs to be synchronized with the corresponding task
We need to make sure tasks assigned to the same worker or the same mounting position don’t overlap. CPO provides the noOverlap constraint for that
forall (s in stations, w in workers) noOverlap (all (t in tasks) aTask[t][s][w]);
forall (m in mounting_positions, s in stations)
noOverlap (all (w in workers, t in tasks : t.mounting_position == m) aTask[t][s][w]); CPO also provides precedence constraints between interval start and end points. In our case when we have a precedence A \prec B what we want is A to end before B starts.
forall (<i, j> in precedences) endBeforeStart(task[<i>], task[<j>]);We add the ergonomics knapsack constraint
forall (s in stations, w in workers)
sum (t in tasks) t.ergonomy * presenceOf(aTask[t][s][w]) <= ergonomy;We used the boolean variable presenceOf(T) that is true when a task is present and false otherwise.
CPO has a more advanced form of temporal knapsack constraint called cumulative but our tests showed the more complex constraint wasn’t in this very simple case better than the simple knapsack
We add the different assignment restrictions
// Same station
forall (<i, j> in same_station, s in stations)
sum (w in workers) presenceOf(aTask[<i>][s][w]) ==
sum (w in workers) presenceOf(aTask[<j>][s][w]);
// Different station
forall (<i, j> in different_station, s in stations)
sum (w in workers) (presenceOf(aTask[<i>][s][w]) + presenceOf(aTask[<j>][s][w])) <= 1;
// Same station and worker
forall (<i, j> in same_worker, s in stations, w in workers)
presenceOf(aTask[<i>][s][w]) == presenceOf(aTask[<j>][s][w]);
// Different station and worker
forall (<i, j> in different_worker, s in stations, w in workers)
presenceOf(aTask[<i>][s][w]) + presenceOf(aTask[<j>][s][w]) <= 1;
// Allowed stations
forall (ts in allowed_stations, s in stations : !(s in ts.stations), w in workers)
presenceOf(aTask[<as.task>][s][w]) == 0;Finally we add the objective constraint that counts the number of used station * worker combinations
dexpr int used [s in stations][w in workers] = or (t in tasks) presenceOf(aTask[t][s][w]);
dexpr int total = sum (s in stations, w in workers) used[s][w];
minimize total;We don’t use the symmetry breaking used by Alghazi as tests (over 1 instance …) showed it slowed down the resolution. On other aspects the difference between the models are fairly small and mainly due to us having more experience with CPO.
The model finds the optimal solution in 1 seconds versus 2 seconds for Alghazi model on a Intel core i5 @1.60Ghz with 8MB
Optimality proof
The only provided instance is so simple that just a global capacity reasoning is enough to close the problem as soon as the optimal solution is found.
sum (t in tasks) t.duration <= total * cycle;Larger instances may require may require stronger lower bounds possibly based on the pack constraint like we have done for the bin-packing version of the assembly-line balancing problem
! --------------------------------------------------- CP Optimizer 20.1.0.0 --
! Minimization problem - 1,350 variables, 569 constraints
! Presolve : 225 extractables eliminated
! LogPeriod = 100,000,000
! Initial process time : 0.06s (0.06s extraction + 0.00s propagation)
! . Log search space : 488.4 (before), 488.4 (after)
! . Memory usage : 7.0 MB (before), 7.0 MB (after)
! Using parallel search with 8 workers.
! ----------------------------------------------------------------------------
! Best Branches Non-fixed W Branch decision
0 1,350 -
+ New bound is 7
! Using iterative diving.
! Using temporal relaxation.
* 17 1,336 0.31s 1 (gap is 58.82%)
* 15 1,338 0.33s 3 (gap is 53.33%)
* 10 683 0.33s 4 (gap is 30.00%)
* 8 1,791 0.33s 7 (gap is 12.50%)
* 7 2,365 1.15s 5 (gap is 0.00%)
! ----------------------------------------------------------------------------
! Search completed, 5 solutions found.
! Best objective : 7 (optimal - effective tol. is 0)
! Best bound : 7
! ----------------------------------------------------------------------------
! Number of branches : 169,600
! Number of fails : 1,588
! Total memory usage : 70.8 MB (69.6 MB CP Optimizer + 1.1 MB Concert)
! Time spent in solve : 1.28s (1.23s engine + 0.06s extraction)
! Search speed (br. / s) : 138,902.5
! ----------------------------------------------------------------------------OPL model
/*********************************************
* OPL 20.1.0.0 Model
* Author: diegoolivierfernandezpons
* Creation Date: Jan 13, 2021 at 5:54:33 PM
*********************************************/
using CP;
//////////////
// Database //
//////////////
tuple task_t {
key int id;
int start;
int end;
int duration;
int mounting_position;
float ergonomy;
}
tuple allowed_station_t {
key int task;
{int} stations;
}
tuple int_pair_t { int a; int b; }
//////////
// Data //
//////////
int nb_workers = ...;
int nb_stations = ...;
{task_t} tasks = ...;
{allowed_station_t} allowed_stations = ...;
int cycle = ...;
int ergonomy = ...;
{int_pair_t} precedences = ...;
{int_pair_t} same_station = ...;
{int_pair_t} different_station = ...;
{int_pair_t} same_worker = ...;
{int_pair_t} different_worker = ...;
///////////
// Model //
///////////
// Indexes
range workers = 1 .. nb_workers;
range stations = 1 .. nb_stations;
{int} mounting_positions = { t.mounting_position | t in tasks };
// Variables
dvar interval task [t in tasks] in t.start .. t.end size t.duration;
dvar interval aTask [t in tasks][s in stations][w in workers] optional in
maxl(t.start, (s - 1) * cycle) .. minl(t.end, s * cycle);
dexpr int used [s in stations][w in workers] = or (t in tasks) presenceOf(aTask[t][s][w]);
dexpr int total = sum (s in stations, w in workers) used[s][w];
minimize total;
constraints {
// Enough capacity for all tasks
sum (t in tasks) t.duration <= total * cycle;
// Tasks assigned to one station * worker
forall (t in tasks) alternative (task[t], all (s in stations, w in workers) aTask[t][s][w]);
// No overlap for workers
forall (s in stations, w in workers) noOverlap (all (t in tasks) aTask[t][s][w]);
// No overlap for mounting positions
forall (m in mounting_positions, s in stations)
noOverlap (all (w in workers, t in tasks : t.mounting_position == m) aTask[t][s][w]);
// Precedences
forall (<i, j> in precedences) endBeforeStart(task[<i>], task[<j>]);
// Ergonomics limits
forall (s in stations, w in workers)
sum (t in tasks) t.ergonomy * presenceOf(aTask[t][s][w]) <= ergonomy;
// Same station
forall (<i, j> in same_station, s in stations)
sum (w in workers) presenceOf(aTask[<i>][s][w]) ==
sum (w in workers) presenceOf(aTask[<j>][s][w]);
// Different station
forall (<i, j> in different_station, s in stations)
sum (w in workers) (presenceOf(aTask[<i>][s][w]) + presenceOf(aTask[<j>][s][w])) <= 1;
// Same station and worker
forall (<i, j> in same_worker, s in stations, w in workers)
presenceOf(aTask[<i>][s][w]) == presenceOf(aTask[<j>][s][w]);
// Different station and worker
forall (<i, j> in different_worker, s in stations, w in workers)
presenceOf(aTask[<i>][s][w]) + presenceOf(aTask[<j>][s][w]) <= 1;
// Allowed stations
forall (ts in allowed_stations, s in stations : !(s in ts.stations), w in workers)
presenceOf(aTask[<ts.task>][s][w]) == 0;
// Symmetry breaking
//forall (s in stations, w in workers : w + 1 in workers) used[s][w + 1] <= used[s][w];
}/*********************************************
* OPL 20.1.0.0 Data
* Author: diegoolivierfernandezpons
* Creation Date: Jan 13, 2021 at 6:22:30 PM
*********************************************/
tasks = {
<1,0,431180,60,1,20>,
<2,60,515000,3300,1,17.91>,
<3,60,444680,13500,1,19.8>,
<4,60,447740,11340,3,19.57>,
<5,60,515000,4020,1,23.6>,
<8,60,515000,24840,3,22.61>,
<9,60,507980,18900,3,35.94>,
<10,18960,515000,7020,1,44>,
<15,0,431180,60,9,20>,
<16,60,511700,3120,7,26.94>,
<17,60,444680,13500,7,19.8>,
<18,60,447740,11340,9,19.57>,
<19,60,515000,23940,9,22.09>,
<21,60,504380,22680,9,35.35>,
<23,22740,515000,10620,7,44>,
<27,3180,515000,3300,9,17.91>,
<29,60,504374,9828,9,18.82>,
<30,60,504878,10008,3,19.04>,
<31,4596,515000,6216,1,19.4>,
<32,5226,515000,6216,7,19.4>,
<33,60,508784,4536,1,10.15>,
<34,60,515000,5724,7,6.62>,
<35,60,515000,11592,7,16.39>,
<38,60,508784,5166,7,9.85>,
<41,60,515000,6264,1,6.82>,
<42,60,515000,12852,1,15.61>,
<44,10068,515000,10122,3,16.18>,
<48,9888,515000,10626,9,14.82>,
<55,13560,515000,70320,1,24.15>,
<56,0,447740,1440,1,24>,
<58,21060,515000,3960,0,24>,
<59,16740,511040,4320,0,46>,
<60,0,495200,5220,0,12>,
<62,5220,506720,11520,0,49>,
<64,13560,515000,70320,7,24.13>,
<65,0,447740,1440,7,24>,
<67,21060,515000,3960,0,24>,
<68,16740,511040,4320,0,46>,
<69,0,495200,5220,0,12>,
<71,5220,506720,11520,0,49>,
<73,11400,515000,67260,3,26.65>,
<74,10068,515000,4200,3,15.64>,
<75,60,515000,13500,3,19.04>,
<78,21480,515000,3960,0,27>,
<79,17160,511040,4320,0,23>,
<80,0,494840,5280,0,12>,
<83,5280,506720,11880,0,90>,
<85,11400,515000,67260,9,26.87>,
<86,9888,515000,4200,9,14.91>,
<87,60,515000,13500,9,19.04>
};
precedences={<1,3>,<1,4>,<1,5>,<1,8>,<1,9>,<9,10>,<15,16>,<15,17>,<15,18>,<15,19>,<15,21>,<21,23>,<15,27>,<15,29>,<1,30>,<33,31>,<38,32>,<1,33>,<15,34>,<15,35>,<15,38>,<1,41>,<1,42>,<30,44>,<29,48>,<3,55>,<62,58>,<62,59>,<60,62>,<17,64>,<71,67>,<71,68>,<69,71>,<4,73>,<30,74>,<1,75>,<83,78>,<83,79>,<80,83>,<18,85>,<29,86>,<15,87>,<16,27>,<59,58>,<68,67>,<56,73>,<79,78>,<65,85>};
nb_workers = 5;
nb_stations = 5;
cycle = 103000;
ergonomy = 500;
same_station = {};
different_station = {};
same_worker = {<58,59>,<59,60>,<60,62>,<67,68>,<68,69>,<69,71>,<78,79>,<79,80>,<80,83>};
different_worker = {};
allowed_stations ={< 8, {1}>, <9, {1}>, <19, {1}>, <21, {1}>, <55, {3}>, <64,{3}> , <73, {4}>, <85, {4}>};References
[1] Bowman, E. H. 1960. “Assembly-Line Balancing by Linear Programming.” Operations Research 8 (3): 385–89.
[2] Falkenauer, Emanuel. (2005). Line balancing in the real world. International Conference on Product Lifecycle Management.
[3] Alghazi, Anas Alsayed, "Balancing and Sequencing of Mixed Model Assembly Lines" (2017). All Dissertations. 2022. https://tigerprints.clemson.edu/all_dissertations/2022
[4] Alghazi, Anas, and Mary E. Kurz. 2018. “Mixed Model Line Balancing with Parallel Stations, Zoning Constraints, and Ergonomics.” Constraints – An International Journal 23 (1): 123–53.




