The quay crane scheduling problem (QCSP) consists in scheduling quay cranes to load and unload containers from ships.

Photo by Jacob Meissner on Unsplash
Quay crane undoubtedly is the most expensive asset in a port. Focus on keeping quay cranes productive is an important step to improve profitability. Lower rate of quay crane transfer operations causes delay in ship and container yard operation. This causes difficulty for recipients and delivery activities. Indirectly, quay crane moves dictates the berth utilisation, turn-around time of ships and then the port performance.
Crane scheduling
Crane scheduling is typically done after the berth assignment problem (BAP) that assigns berth positions and arrival / departure times to ships.
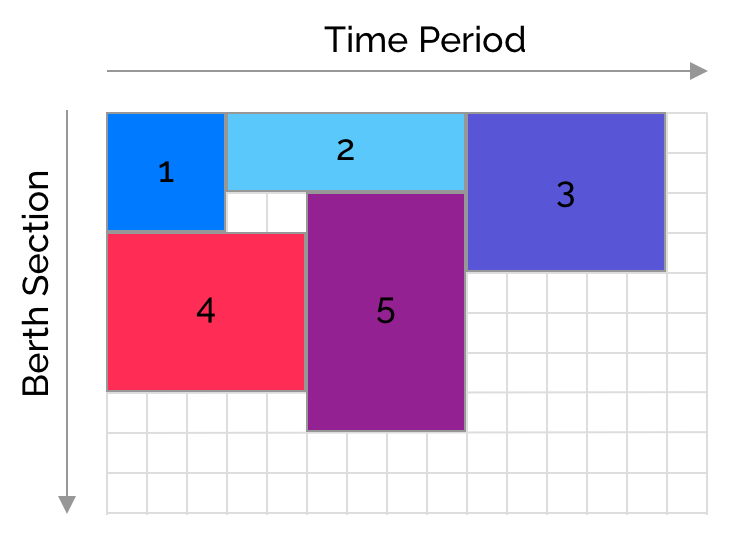
Container movements are grouped into holds (batches) in order to make the problem easier to tackle. Therefore each ship is associated with a number of holds that need to be assigned to a crane. Each hold has a specific a position or bay
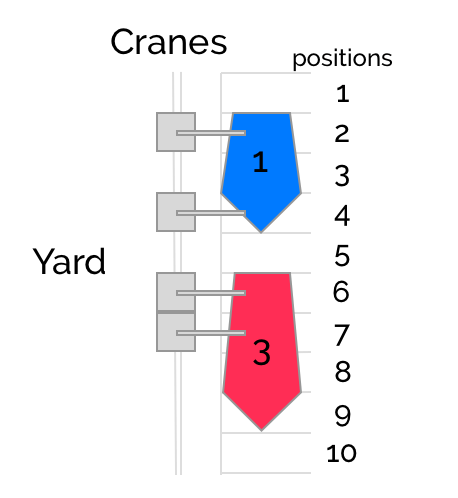
Quay cranes are mounted on a single rail which prevents them to crossing. Because of this fact, and depending on the policy of the port, cranes can be blocked on a hold (meaning a single crane will execute all the container movements in that hold) or shifted across holds. Depending on the length of the holds, moving the cranes along the berth may be negligible or not.
Problem Statement
The crane scheduling problem can be seen as a scheduling problem with side constraints to prevent crossing of cranes.
We make the following assumptions and simplifications:
- The arrival and departure times of the ships have been fixed
- The berthing positions of the boats are already fixed
- Each boat has zero or one hold per bay (for simplicity we don’t divide the unloading of containers from the same bay into multiple tasks)
- No precedences required on the holds
- Quay cranes cannot cross over each other
- Only one quay crane can work on a hold at a time until it completes the hold
We will use berthing data corresponding to the example above
| Ship | Length | Docking position | Arrival | Departure |
|---|---|---|---|---|
| 1 | 3 | 0 | 0 | 3 |
| 2 | 2 | 0 | 3 | 9 |
| 3 | 4 | 0 | 9 | 14 |
| 4 | 4 | 3 | 0 | 4 |
| 5 | 6 | 2 | 5 | 9 |
And the following (un)loading tasks
| Ship | Bay | Processing time |
|---|---|---|
| 1 | 0 | 3 |
| 1 | 1 | 3 |
| 1 | 2 | 2 |
| 2 | 0 | 5 |
| 2 | 1 | 5 |
| 3 | 0 | 5 |
| 3 | 1 | 5 |
| 3 | 2 | 4 |
| 3 | 3 | 1 |
| 4 | 0 | 1 |
| 4 | 1 | 2 |
| 4 | 3 | 1 |
| 5 | 0 | 2 |
| 5 | 1 | 1 |
| 5 | 3 | 3 |
CPO formulation
CP Optimizer provides a special form of variable named intervals to model tasks to be scheduled. An interval has
- a presence flag : bool
- a start : int
- a duration : int+
We will model the (un)loading tasks, and the ship docking as intervals.
range horizon = min (s in ships) arrival[s] .. max (s in ships) departure[s];
dvar interval docking [ships] in horizon;
dvar interval load [t in tasks] in horizon size duration[t];Start and end dates
We want to express the fact that a ship cannot be docked before its arrival time and after its departure time. We can do that either as constraints
forall (s in ships) startOf(docking[s]) >= arrival[s];
forall (s in ships) endOf(docking[s]) <= departure[s];Or we can write it directly in the definition of the docking interval
dvar interval docking[s in ships] in arrival[s] .. departure[s];Spans
We want to express the fact that each ship will be docked for as long as there are (un)loading tasks to be performed. This is done with a span constraint
forall (s in ships) span (docking[s], all (t in tasks : t.ship == s) load[t]);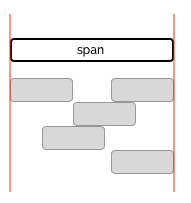
Alternatives
Now we want to assign tasks to different cranes. This is done by creating a copy of each task for each crane and adding an alternative
dvar interval load_on [tasks][cranes] optional;
forall (t in tasks) alternative (load[t], all (c in cranes) load_on[t][c])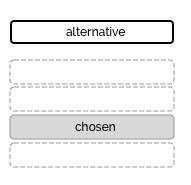
The alternative is equivalent to an OR between the presence values of the load-on-crane tasks : presenceOf(load_on[t][1]) + presenceOf(load_on[t][2]) + .. == 1 combined with a constraint forcing the simultaneity between load[t] and load_on[t][c].
Sequences and noOverlap
We don’t want a crane to be assigned two (temporally) overlapping tasks. To avoid this we want to add a no-overlap constraint over all intervals done by each crane. This is done by
- defining for each crane a sequence with the tasks potentially done by that crane
- adding a no overlap constraint on the sequence
dvar sequence crane[c in cranes] in all (t in tasks) load_on[t][c];
forall (c in cranes) noOverlap(crane[c]);Setup times
To model the time it takes to move a crane from position p to position q we will add a setup time equal to \mid \; p - q\; \mid. This is done by adding type to the intervals in each sequence and distance matrix to the noOverlap constraint.
In our case the type is just the position of each task. The position however needs to be computed as the addition of the bay (relative to the boat) and the position of the boat (relative to the dock).
int offset [ships] = [ d.ship : d.position | d in docking ];
int position [t in tasks] = t.bay + offset[t.ship]
tuple setup_t { int a; int b; int dist; }
{setup_t} movement_time = {<p, q, ftoi(abs(p - q))> | p, q in positions : p != q }
dvar sequence crane[c in cranes] in all (t in tasks) load_on[t][c] type position;
forall (c in cranes) noOverlap (crane[c], movement_time);
Model
/*********************************************
* OPL 12.10.0.0 Model
* Author: diegoolivierfernandezpons
* Creation Date: Nov 20, 2020 at 6:28:03 PM
*********************************************/
using CP;
tuple task_t { int ship; int bay; int duration; }
tuple position_t { int ship; int length; int position; int arrival; int departure; }
int num_crane = ...;
int quay_positions = ...;
{task_t} tasks = ...;
{position_t} docking = ...;
range cranes = 1 .. num_crane;
range positions = 0 .. quay_positions - 1;
{int} ships = { s | <s, l, p, a, d> in docking };
int arrival [ships] = [s : a | <s,l,p,a,d> in docking ];
int departure [ships] = [s : d | <s,l,p,a,d> in docking ];
int offset [ships] = [s : p | <s,l,p,a,d> in docking ];
int position [t in tasks] = t.bay + offset[t.ship];
range horizon = min (s in ships) arrival[s] .. max (s in ships) departure[s];
tuple setup_t { int a; int b; int duration; }
{setup_t} distance = {<p, q, ftoi(abs(p - q))> | p, q in positions: q != p };
dvar interval docked [s in ships] in horizon;
dvar interval load [<s, b, d> in tasks] size d;
dvar interval load_on [tasks][cranes] optional;
dvar sequence crane [c in cranes] in all (t in tasks) load_on[t][c] types position;
minimize max (t in tasks) endOf(load[t]);
constraints {
// Ship arrival and departure
forall (s in ships) startOf(docked[s]) == arrival[s];
forall (s in ships) endOf(docked[s]) <= departure[s];
// loading a ship is done while the ship is docked
forall (s in ships) span (docked[s], all (<s, b, d> in tasks) load[<s, b, d>]);
// Each loading task is done only by one crane
forall (t in tasks) alternative (load[t], all(c in cranes) load_on[t][c]);
// Cranes cannot be assigned overlapping tasks
forall (c in cranes) noOverlap (crane[c], distance);
}Data
num_crane = 4;
quay_positions = 10;
tasks = {
<1,0,3>, <1,1,3>, <1,2,2>,
<2,0,5>, <2,1,5>,
<3,0,5>, <3,1,5>, <3,2,4>, <3,3,1>,
<4,0,1>, <4,1,2>, <4,3,1>,
<5,0,2>, <5,1,1>, <5,3,3>
};
docking = {
<1, 3, 0, 0, 3>
<2, 2, 0, 3, 8>
<3, 4, 0, 9, 14>
<4, 4, 3, 0, 5>
<5, 6, 2, 5, 9>
};Result
! -------------------------------------------------- CP Optimizer 12.10.0.0 --
! Minimization problem - 84 variables, 39 constraints
! Initial process time : 0.01s (0.01s extraction + 0.00s propagation)
! . Log search space : 45.6 (before), 45.6 (after)
! . Memory usage : 677.0 kB (before), 677.0 kB (after)
! Using parallel search with 4 workers.
! ----------------------------------------------------------------------------
! Best Branches Non-fixed W Branch decision
0 84 -
+ New bound is 14
! Using iterative diving.
* 14 101 0.03s 1 (gap is 0.00%)
! ----------------------------------------------------------------------------
! Search completed, 1 solution found.
! Best objective : 14 (optimal - effective tol. is 0)
! Best bound : 14
! ----------------------------------------------------------------------------
! Number of branches : 23092
! Number of fails : 787
! Total memory usage : 3.8 MB (3.3 MB CP Optimizer + 0.5 MB Concert)
! Time spent in solve : 0.04s (0.02s engine + 0.01s extraction)
! Search speed (br. / s) : 769734.1
! ----------------------------------------------------------------------------
load = [ edited ... ]
docked = [<1 0 3 3> <1 3 8 5> <1 9 14 5> <1 0 5 5> <1 5 9 4>];
load_on = [ edited ... ]
crane = [{
<"load_on[<4,1,2>][1]" 0 10 4 0 2 2>
<"load_on[<4,3,1>][1]" 1 11 6 4 5 1>
<"load_on[<5,3,3>][1]" 2 14 5 6 9 3>
<"load_on[<3,3,1>][1]" 3 8 3 11 12 1>
} {
<"load_on[<1,2,2>][2]" 0 2 2 0 2 2>
<"load_on[<4,0,1>][2]" 1 9 3 3 4 1>
<"load_on[<5,0,2>][2]" 2 12 2 5 7 2>
<"load_on[<5,1,1>][2]" 3 13 3 8 9 1>
<"load_on[<3,2,4>][2]" 4 7 2 10 14 4>
} {
<"load_on[<1,1,3>][3]" 0 1 1 0 3 3>
<"load_on[<2,1,5>][3]" 1 4 1 3 8 5>
<"load_on[<3,1,5>][3]" 2 6 1 9 14 5>
} {
<"load_on[<1,0,3>][4]" 0 0 0 0 3 3>
<"load_on[<2,0,5>][4]" 1 3 0 3 8 5>
<"load_on[<3,0,5>][4]" 2 5 0 9 14 5>
}];
The output format of docked
- presence flag
- start time
- end time
- duration
with the convention that the endtime is open
The output format ofcrane
- rank in the sequence
- index in the original (tasks) array
- type (position)
- start time
- end time
- duration
The rank in the sequence may not follow the chronological order. We need to add an extra constraint to CPO if we what that.
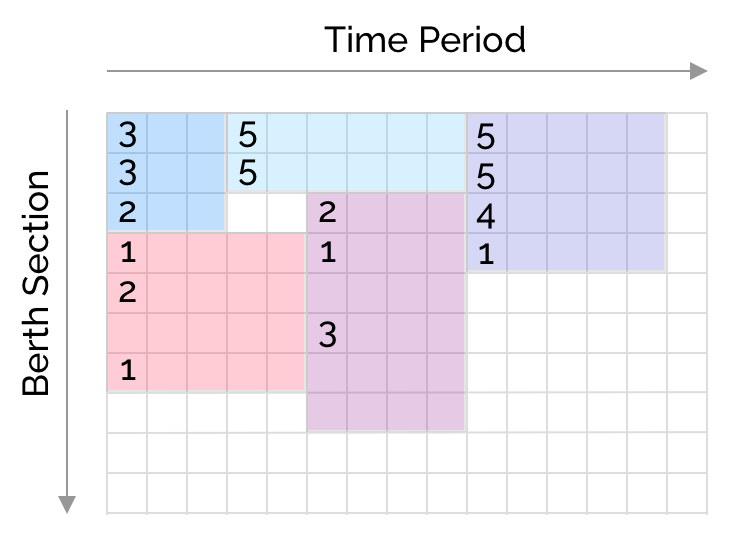
The solution looks like this
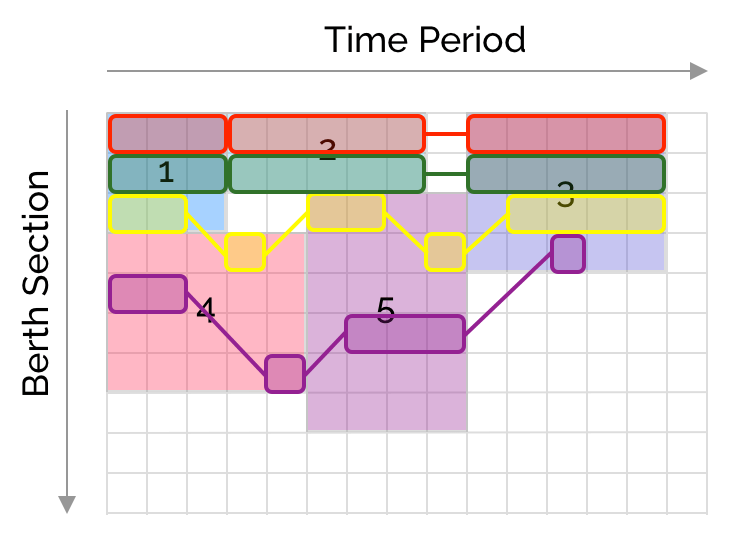
Interestingly the model readjusted the end times of ship 2 showing the ship can depart earlier than originally planned.
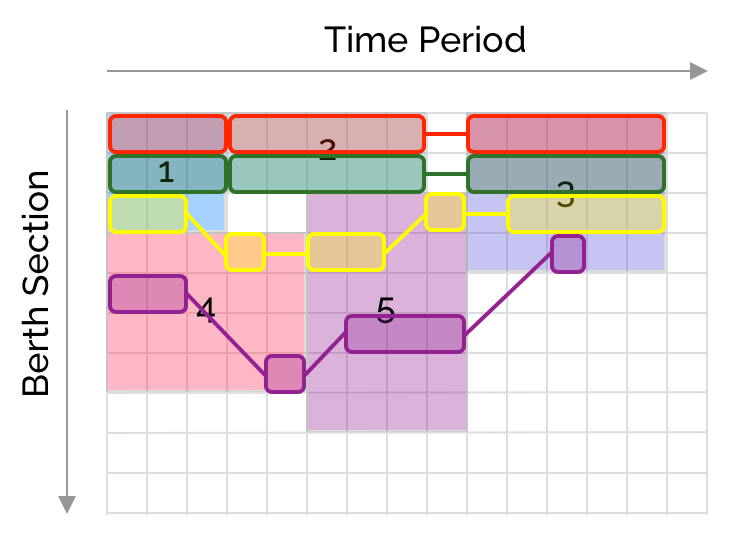
We also notice the solution doesn’t minimize the number of crane movements : reversing the intervals in ship 5 for crane 3 (yellow) achieves the same makespan with 2 less movements
Possible improvements
Several improvements are possible in this model
- lexicographic minimization makespan followed by lateness
- minimization of the movements of cranes
- explicit constraint preventing crane cross over
Also we could let the engine decide when to dock the ships
If we still retain the assigned positions, then each position creates a noOverlap constraint
// Non overlap of docking ships
forall (p in positions) noOverlap (all (t in tasks : position[t] == p) docked[t.ship]);If we also ignore the assigned positions then we are solving the combined berth and quay crane scheduling problem (BQCSP)




