Shift-scheduling models are very common in workforce optimization.
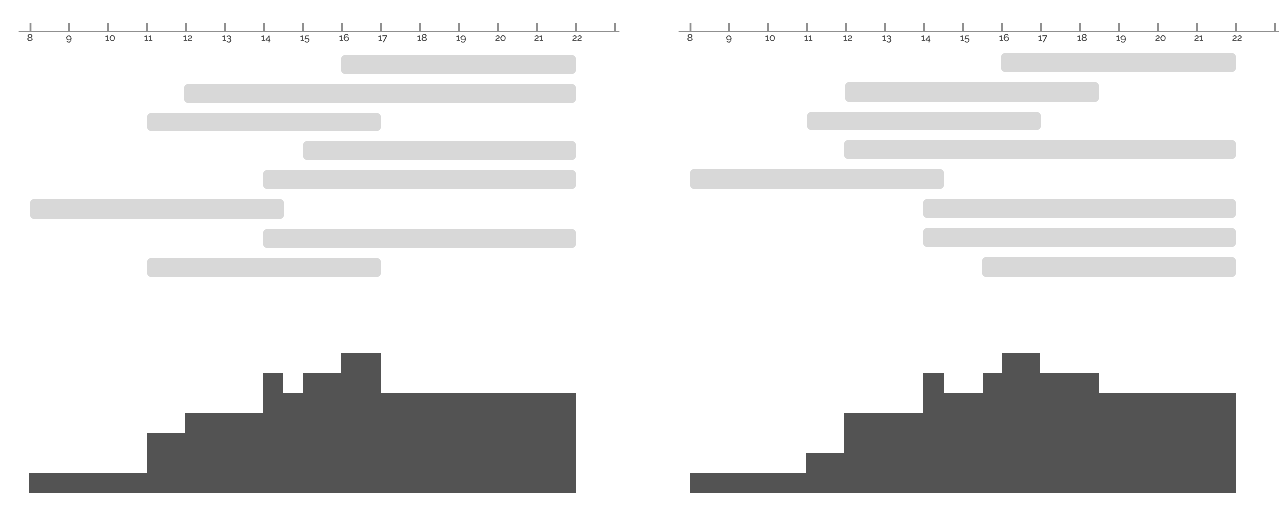
Employees are scheduled over one or multiple weeks, in order to cover the demand. Each employee has a contract that specifies the number of days and total hours worked, and the minimum and maximum length of a shift.
Basic MIP model
The core idea behind MIP models in shift-scheduling is to create a set of possible shifts S = \lbrace (start\_time, duration) \rbrace and one boolean variable for each shift x employee combination x^e_s \in \lbrace 0, 1 \rbrace
The MIP model becomes a covering problem where the engine needs to choose which boolean variables to set to 1 to obtain the best possible coverage of the demand (1), while respecting constraints between the shifts selected for each employee
- total number of shifts (2)
- total number of hours (3)
- minimum distance between shifts (4)
The model can be written
\begin{aligned}
\min \sum_{t\, \in\, time} \left \lbrack D_t - \sum_e \sum_{t\, \in\, s} x^e_s \right \rbrack^+ & \quad (1)\\
\\
\forall e \quad \sum_s x^e_s = \mathrm{Days}^e & \quad (2)\\
\forall e \quad \sum_s h_s x^e_s = \mathrm{Hours}^e & \quad (3)\\
\forall e\, \forall s, u \quad \mathrm{dist}(s, u) \lt \underline{d} \Rightarrow x^e_s + x^e_u \leq 1 & \quad (4)\\
\\
x^e_s \in \lbrace 0, 1 \rbrace &
\end{aligned}Where ^+ is the positive part of the expression in other words e \rightarrow \max(0, e)
Practical considerations
While the theory is simple, in practice shift-scheduling models generate a very large amount of boolean variables and constraints. Therefore it is imperative to use the specifics of the problem to reduce as much as possible the number of variables and constraints.
Typical aspects that can be improved are
- The number of boolean variables: in general an employee is not elegible for all shifts for reasons ranging from specific provisions in his / her contract, to personal preference. It is fundamental for good performance to avoid generating shift variables that are provably equal to zero. One might think the engine preprocessor will remove those variables (which is the case) but while it is doing those simplifications it is not doing other ones, and it may fail to see other improvements for being busy removing useless variables
- The number of conficts constraints (4) : it is important to avoid generating constraints that are provably satisfied, for instance when two shifts are distant of more than the minimum inter-shift time, there is no point in adding a confict constraint
Positive part of an expression
The positive part expression \lbrack A - B \, \rbrack^+ can be linearized by adding negative and positive delta variables to the equality constraint
\begin{aligned}
A - B = - negative + positive &\\
negative, positive \geq 0 &\\
\end{aligned}The variables can be floating point variables without any loss of generality. One has just to be careful with the compensation between N and P for instance 10 - 5 = -2 + 7 The positive part of the expression is 5, not 7.
When the positive part is used in a minimization objective, there is no need to worry about compensation. Otherwise some extra precautions need to be taken.
MIP model with contract types
A useful improvement of the basic model is to add a contract selection dimension : the engine will also choose for each employee the most adapted contract, if any.
For instance
- full timer : 40h of work, 5 days of work
- part timer : 25h of work, 3 days of work
We introduce new boolean variables y^e_c \in \lbrace 0, 1 \rbrace that indicate the contract c is used for employee e
\begin{aligned}
\min \sum_{t\, \in\, time} \left \lbrack D_t - \sum_e \sum_{t\, \in\, s} x^e_s \right \rbrack^+ & \quad (1)\\
\\
\forall e \quad \sum_s x^e_s = \sum_c \mathrm{Days}_c * y_c^e & \quad (2)\\
\forall e \quad \sum_s h_s x^e_s = \sum_c \mathrm{Hours}_c * y_c^e & \quad (3)\\
\forall e\, \forall s, u \quad \mathrm{dist}(s, u) \lt \underline{d} \Rightarrow x^e_s + x^e_u \leq 1 & \quad (4)\\
\forall e \quad \sum_c y^e_c \leq 1 & \quad (5)
\\
\\
x^e_s \in \lbrace 0, 1 \rbrace, \quad y^e_c \in \lbrace 0, 1 \rbrace & \\
\end{aligned}Constraints (2) and (3) respectively say the number of worked days and the number of worked ours is equal to what is specified in the contract. Constraint (5) says at most one contract can be assigned to any employee.
Multi-criteria optimization
With the introduction of the contract type – and the fact that some employees may not be assigned any contract if their presence is not necessary, we create two conflicting objectives
- coverage will tend to increase the number of employees
- cost will tend to decrease the number of employees
In general demand is not very precise as it is the result of a forecast algorithm on historical data, processed with employee average productivity. Therefore, having a full coverage of the demand is not absolutely required.
Hence a limit on the demand undercoverage can be added while optimizing for cost.
\displaystyle\forall t \quad D_t - 1 \leq \sum_e \sum_{t \in s} x^e_sThese types of hard constraints should be used with care as they may make the problem infeasible. A better approach is to create an objective that stops improving at the desired threshold \theta
\begin{aligned}
\forall t \quad D_t - \left \lbrack \sum_e \sum_{t \in s} x^e_s \right \rbrack - \theta \leq z\\
z \geq 0
\end{aligned}The engine will minimize z until z = 0 in which case the minimization stops with
\displaystyle\forall t \quad D_t - \theta \leq \sum_e \sum_{t \in s} x^e_swhile if z cannot reach 0 the engine will (try to) find the best possible z
Now z can be used in a lexicographic optimization
\begin{aligned}
\min \mathrm{lex}\, (z, cost, under)\\
\\
\forall t \quad D_t - \left \lbrack \sum_e \sum_{t \in s} x^e_s \right \rbrack - \theta \leq z\\
cost = \sum^{}_e cost_c * y^e_c\\
under = \sum_{t\, \in\, time} \left \lbrack D_t - \sum_e \sum_{t\, \in\, s} x^e_s \right \rbrack^+
\end{aligned}Which instructs the engine to
- bring for each time period the coverage to be at least theta from the demand
- then minimize the total cost of the contracts
- then minimize the under-coverage
Lexicographic minimization of deviations from a target is actually reminiscent of goal programming
Shift length
Contracts often include restrictions on the possible shift lengths
- full timer : between 6h and 10h per shift
- part timer : between 4h and 8h per shift
It is important for performance reasons to avoid duplication of shifts, for instance a shift of 6h for the full time contract s_1 and a shift of 6h for the part time contract s_2 leading to two indistinguable variables x^e_{s_1} and x^e_{s_2}
Instead a set of incompatible contracts I_s for each shift s and the following constraint can be added
\displaystyle\forall s \, \forall e \quad x^e_s + \sum_{c \in I_s} y^e_c \leq 1OPL model
We have defined generic parameters for the model to be easily used in various contexts like monthly or weekly scheduling (change range weeks = 1 .. 1 to range weeks = 1 .. 4), time granularity from 1h to 15 minutes (change range hours = 6 .. 24 to range hours = 36 .. 96), min time between schedules, etc.
/*********************************************
* OPL 20.1.0.0 Model
* Author: diegoolivierfernandezpons
* Creation Date: Dec 22, 2020 at 6:20:08 PM
*********************************************/
// Parameters
int inter_shift = 12;
range weeks = 1 .. 1;
range days = 0 .. 6;
range hours = 6 .. 24;
int undercoverage_tolerance = 1;
// Data
tuple contract_t { int days; int hours; int min_hours; int max_hours; }
{contract_t} contracts = { <5, 40, 5, 10>, <3, 25, 6, 10> };
int demand [w in weeks][d in days][h in hours] = rand(10);
{string} employees = {
"Alice", "Bob", "Charlie", "Diana", "Eleonor", "Frida", "Gilles", "Helena", "Irina", "Jasmin",
"Keith", "Lily", "Mathias", "Nathalie", "Olga", "Patricia", "Quinn", "Ralf", "Samatha", "Taylor",
"Ulrich", "Vanessa", "William", "Xavier", "Yannis", "Zoe"
};
// Indexes and helpers
range duration = min (c in contracts) c.min_hours .. max (c in contracts) c.max_hours;
tuple shift_t { int start; int duration; }
{shift_t} shifts = { < s, d > | s in hours, d in duration : s + d - 1 in hours };
{int} incompatible [s in shifts] = { ord (contracts, c) | c in contracts : s.duration not in c.min_hours .. c.max_hours };
int last_day = max (d in days) d;
///////////
// Model //
///////////
dvar boolean contract [employees][contracts];
dvar boolean use [employees][weeks][days][shifts];
dvar float+ over [weeks][days][hours];
dvar float+ under [weeks][days][hours];
dvar float+ z;
dexpr float undercoverage = sum (w in weeks, d in days, h in hours) under[w][d][h];
dexpr float cost = sum (e in employees, w in weeks, c in contracts) c.hours * contract[e][c];
minimize staticLex (z, cost, undercoverage);
constraints {
// Undercoverage threshold
forall (w in weeks, d in days, h in hours)
under[w][d][h] - undercoverage_tolerance <= z;
// Each employee has at most one contract
forall (e in employees) sum (c in contracts) contract[e][c] <= 1;
// At most one shift per day per employee
forall (e in employees, w in weeks, d in days) sum (s in shifts) use[e][w][d][s] <= 1;
// Number of days in the contract
forall (e in employees, w in weeks) sum (d in days, s in shifts) use[e][w][d][s]
== sum (c in contracts) c.days * contract[e][c];
// Number of hours in the contract
forall (e in employees, w in weeks) sum (d in days, s in shifts) s.duration * use[e][w][d][s]
== sum (c in contracts) c.hours * contract[e][c];
// Compute under and over coverage
forall (w in weeks, d in days, h in hours)
sum (e in employees, <s, dur> in shifts : s <= h && h < s + dur) use[e][w][d][<s, dur>]
== demand[w][d][h] + over[w][d][h] - under[w][d][h];
// Minimum distance between shifts within a week
forall (e in employees, w in weeks, d in days : d + 1 in days, s1, s2 in shifts :
s1.start + s1.duration + inter_shift > 24 + s2.start)
use[e][w][d][s1] + use[e][w][d + 1][s2] <= 1;
// Minimum distance between shifts between weeks
forall (e in employees, w in weeks : w + 1 in weeks, s1, s2 in shifts :
s1.start + s1.duration + inter_shift > 24 + s2.start)
use[e][w][last_day][s1] + use[e][w + 1][0][s2] <= 1;
// Incompatible shifts and contracts
forall (e in employees, w in weeks, d in days, s in shifts : card(incompatible[s]) > 0)
sum (c in contracts : ord(contracts, c) in incompatible[s]) contract[e][c]
+ use[e][w][d][s] <= 1;
}To visualize the results directly in IBM ILOG OPL Cplex Studio, we add an ASCII output
tuple sol { int start; int duration; }
sorted {sol} used [e in employees] = { <w * 7 * 24 + d * 24 + s.start, s.duration> | s in shifts, w in weeks, d in days : use[e][w][d][s] == 1 };
range horizon = min (e in employees, s in used[e]) s.start .. max (e in employees, s in used[e]) (s.start + s.duration);
int present [h in horizon][e in employees] = sum (<s, u> in used[e] : s <= h && h < s + u) 1;
execute {
// Shifts
for (var e in employees) {
write (e.charAt(0), " ")
for (var w in weeks) {
for (var d in days) {
for (var h in hours)
if (present[w * 7 * 24 + d * 24 + h][e]) write ("X"); else write (" ")
write ("|")
}
write("|")
}
writeln("")
}
// Coverage
write (" ")
for (var w in weeks) {
for (var d in days) {
for (var h in hours) write (Math.round(under[w][d][h]))
write ("|")
}
write ("|")
}
}Cplex Studio 20.1.0.0 running on a i5-10210U @ 1.6Ghz runs for 40 seconds
The result should be similar to
// solution (multi-objective optimal) with objective 0
A XXXXXXXXXX |XXXXXXXXXX |XXXXX | | XXXXX | | XXXXXXXXXX ||
B XXXXXXXX | | | XXXXXXXXXX | XXXXXXX | | ||
C | | | | | | ||
D |XXXXXXXXXX | XXXXXXXXXX| XXXXX| | XXXXXXXXXX | XXXXX||
E XXXXXX |XXXXXXXXXX | XXXXXXXXX| | | | ||
F XXXXXX | |XXXXX | XXXXXXXXX| | XXXXXXXXXX | XXXXXXXXXX ||
G | |XXXXXXXXX | XXXXXXX | XXXXX | XXXXXXXXXX | XXXXXXXXX ||
H XXXXXX |XXXXXXXXXX |XXXXXXXXX | XXXXXXX | XXXXXXXX | | ||
I XXXXXX | |XXXXXXXXX | XXXXXXXXX | |XXXXXX | XXXXXXXXXX ||
J XXXXXXXXXX | XXXXXXXXXX| XXXXXXXXXX | XXXXX| |XXXXX | ||
K XXXXXX |XXXXXXXX |XXXXXXXXX | XXXXXXXXXX |XXXXXXX | | ||
L XXXXXX | | XXXXXXXXX| XXXXX| XXXXXXXXXX | |XXXXXXXXXX ||
M XXXXXXXXX | XXXXXXXX| | |XXXXXXX |XXXXXX | XXXXXXXXXX||
N XXXXXXXXX | | | XXXXXXXXX| XXXXXXXXXX | XXXXXX | XXXXXX||
O | XXXXXXXXXX| | XXXXXXXXXX |XXXXXXX |XXXXX | XXXXXXXX||
P XXXXXXXX | XXXXXXXXXX| XXXXXXXXXX| |XXXXXXX | | XXXXX||
Q | XXXXXXXX| XXXXXXXXXX| XXXXXXX| XXXXXXXX | XXXXXXX | ||
R |XXXXXXXXXX | XXXXXXXXXX| XXXXX | XXXXX | | XXXXXXXXXX ||
S | | | | | | ||
T |XXXXXXXX |XXXXXXXXX | XXXXX| XXXXXXXX | |XXXXXXXXXX ||
U |XXXXXXXXXX | | XXXXXXX |XXXXXXX | XXXXXXXX | XXXXXXXX||
V | |XXXXXXXX | |XXXXXXX | XXXXXXXXXX | ||
W | | | | | | ||
X XXXXXXXXXX | XXXXXXXX| XXXXXXXXX| | XXXXXXX | XXXXXX | ||
Y XXXXXX | XXXXXXXX| | XXXXXXXXXX| |XXXXXX | XXXXXXXXXX ||
Z | | | | | | ||
0000010000000001010|0000101100000001101|1000000000101000010|0000000010000000001|0100010000000001010|0010000000001000000|0010000010000010001||